【仕事に役立つ数学: AI時代に差がつく】感想・レビュー

はじめまして、はるパパです。

さて本日は、
コチラの本をご紹介します。

『仕事に役立つ数学: AI時代に差がつく』

仕事でよく使うExcel関数は何ですか？

データ分析やレポート作成で、
①～③を使う人は多いですね。

たとえば、
①で数値を合計し、
②で平均を出すのはよく見かけます。

でも、
その平均値おかしくない？
って思う時があります。

プロ野球選手の平均年俸、
AとBのケースを考えてみます。

AもBも平均1億ですが、
Aは違和感ありますよね。

2億6500万のスター選手の年俸、
他2名の2軍選手と全然違います。

このように平均だけ見ると、
だまされてしまうこともあります。

では、
どうすればいいでしょうか？

正確なデータ分析やレポート作成用に、
もっとExcel関数を覚えればいい。

でも、
Eccel関数は難しくて覚えにくい。

どんな時にどのような関数を使うのか？
よくわからない。

そんな方にオススメなのが、
コチラの本です。

『仕事に役立つ数学: AI時代に差がつく』

仕事に活用できるExcel関数、
本書に数多く書かれています。

たとえば、
①～⑤のExcel関数も書かれています。

数学の授業で聞いたような気がしますが、
私は全然覚えてなかったです。

プロ野球選手の平均年俸ですが、
平均よりも③の方がわかりやすいです。

データに大きなバラつきがある時は、
③で表すと視覚的に一発でわかる。

データ分析や資料作成で③を使う人、
あまりいないですよね。

もしあなたが③を使えば、
それだけで一目置かれるでしょう。

会社での評価は上がり、
昇進や給料アップにつながります。

Excel関数を使いこなすだけで、
その後の人生が変わります。

人生を変えるExcel関数を学ぶなら、
ぜひ本書をご覧ください。

それでは本書の感想・レビュー、
ブログで紹介します。

皆様の参考になれば幸いです。

第1章：「割合」で目標を可視化する

第1章で参考になると思った箇所、
コチラです。

平均と言えば、
①のイメージですよね。

本書の例を参考にすると、
コチラの平均給与額です。

AVERAGE関数は一般的なので、
仕事で使う人も多いですよね。

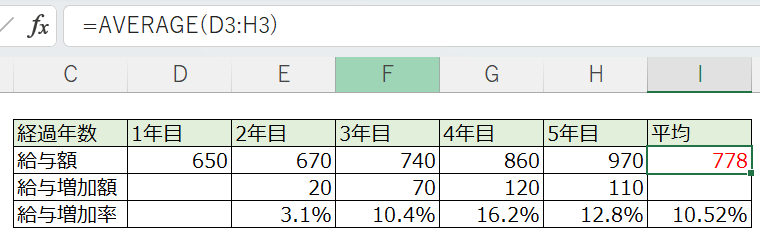
では、
給与増加率の平均は何％でしょうか？

このような増加率の平均を求める場合、
②を使います。

②はGEOMEAN関数を使いますが、
仕事で使う人をあまり見たことない。

赤字を求める関数、
↓の数式をぜひ参考にしてください。

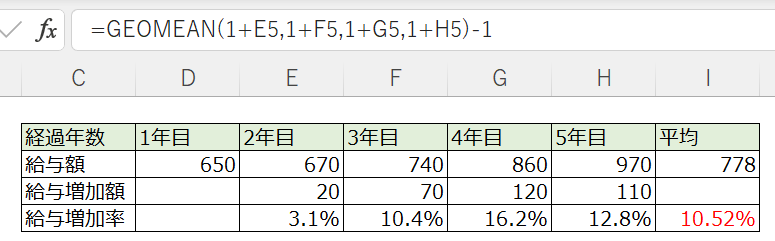
ちなみに、
②を導くExcel関数、
本書には掲載されていませんでした。

もちろん私も知らなかったので、
ChatGPTに聞いてみました。

ChatGPTは丁寧に教えてくれるので、
Excel関数を覚えなくても大丈夫。

Excel関数がわからず困った場合は、
無料のChatGPT先生に聞きましょう。

②幾何平均を導くと、
将来の予測に役立ちます。

たとえば、
この先の予想給与額ですね。

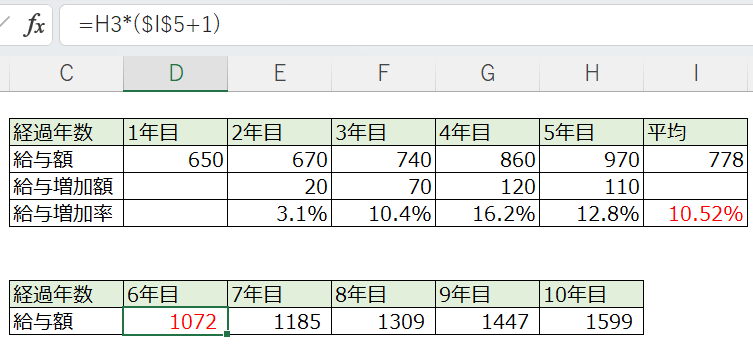
②幾何平均の増加率ずつ、
給与が増加する場合の試算です。

6年目の金額は、
5年目の金額×幾何平均です。

この計算はいろいろな予測に活用でき、
試算のプロとして一目置かれますね。

いままでの計算式、
ぜひ参考にしてください。

第2章：「相関」が見えれば未来がわかる

第2章で参考になると思った箇所、
コチラです。

本書の例をもとに説明します。

たとえば、
あるシーズンの最高気温と、
かき氷の販売数の関係を調べるとします。

Excelに最高気温と販売数を入力し、
選択します。

そして赤枠をクリックすれば、
散布図の出来上がりです。

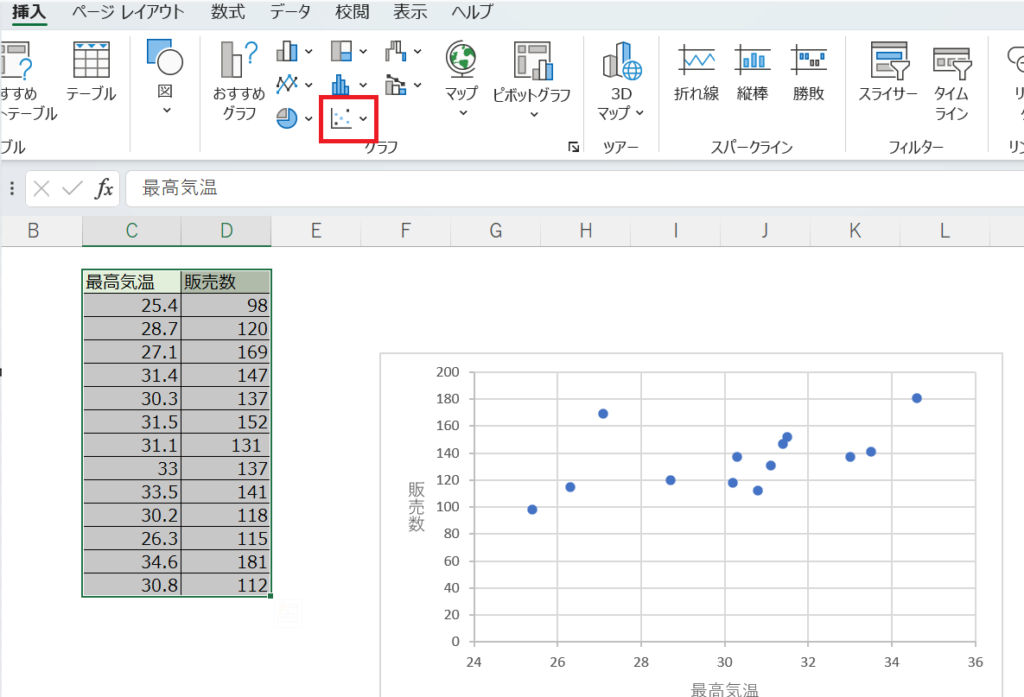
散布図の点を右クリックすると、
「近似曲線の追加」が表示されます。

そこから線形近似を選択すると、
散布図に直線が引かれます。

これが回帰直線です。

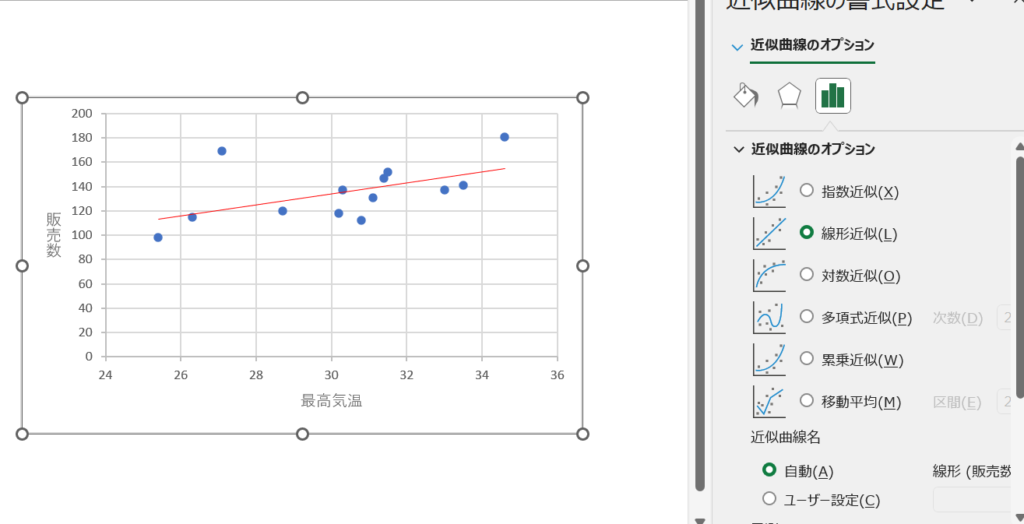
さらに回帰直線をクリックすると、
「近似曲線の書式設定」が表示されます。

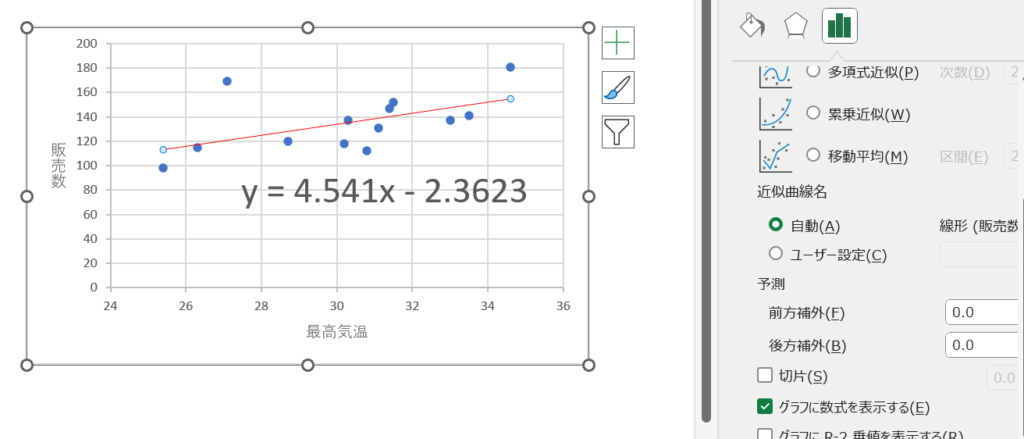
そこで、
「グラフに数式を表示する」を✓すると、
回帰直線の関数が表示されます。

Xに気温を入れると、
販売数が予測できるようになるのです。

これは仕事で使えますよね。

回帰分析で販売数を予測しました、
と報告したら間違いなく一目置かれます。

散布図と回帰直線は簡単なので、
ぜひお試しください。

第3章：「データ」を正しく読み解く

第3章で参考になると思った箇所、
コチラです。

データに大きなバラツキがあると、
平均にだまされることがあります。

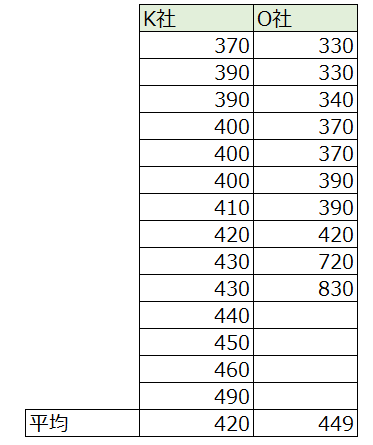
本書の例を借りると、
K社とO社の年収平均をご覧ください。

あまり差がないように見えますが、
実は大きな違いがあります。

K社は最大でも490万ですが、
O社の最大だと830万もあります。

平均は大差なくても、
O社の方が年収幅が大きいのです。

ヒストグラムで見ると、
両社のバラツキが一目瞭然です。

先ほどの表の横に、
年収幅の範囲ごとの件数を数えます。

少し面倒なExcel関数になってますが、
一度作れば他の行にコピペできます。

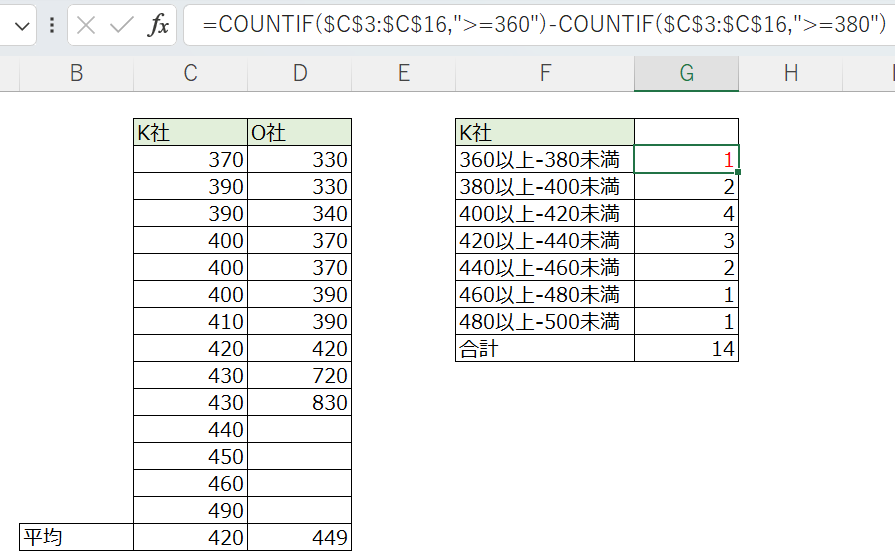
そこから棒グラフを作ると、
こうなります。

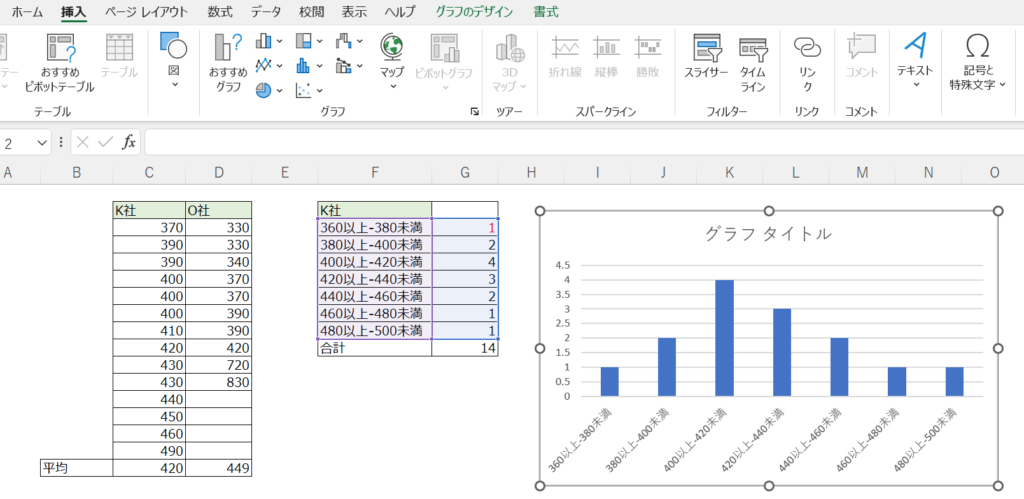
棒グラフ同士の間隔を詰めるには、
右クリックで「データ系列の書式」を選択。

要素の間隔＝0％にして、
体裁を整えるとこうなります。

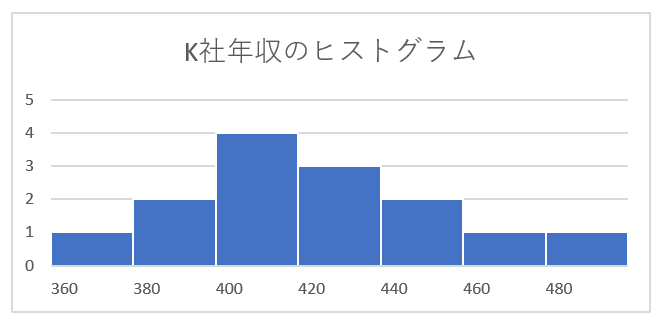
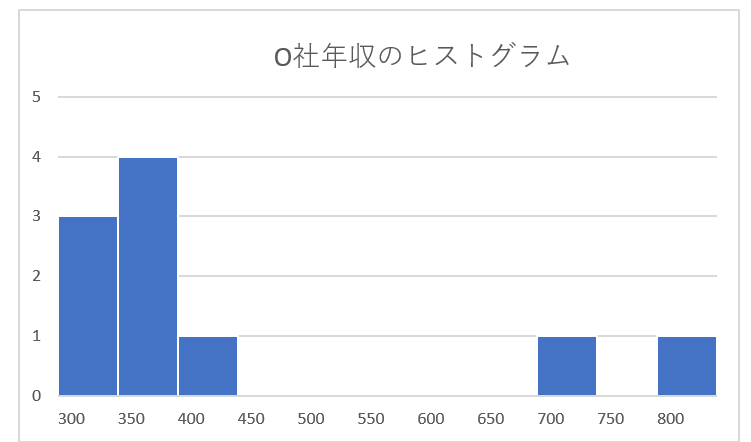
同様にO社のヒストグラムを作成すると、
こうなります。

年収のバラツキがよくわかりますよね。

平均と聞くと、
真ん中くらいのイメージがあります。

しかし、
データにバラツキが大きいと、
平均＝真ん中とは限らないです。

平均を使うケース、
仕事で頻繁に発生すると思います。

その時、
データのバラツキが大きければ、
ヒストグラムで表す方が正確です。

数字のプロと一目置かれ、
あなたの評価は急上昇でしょう。

ぜひご活用ください。

第4章：直近のトレンドを読む

第4章で参考になると思った箇所、
コチラです。

時系列データを扱う場合、
変動要因が入りこんでいます。

その変動要因によって、
数字が大きく変動します。

この変動要因をなるべく排除し、
全体のトレンドを見る場合、
移動平均を使います。

たとえば、
7日平均とか25日平均とか、
投資家なら見たことありますよね。

試しに、
2024/4/1～2024/7/24の期間で、
日経平均のトレンドを見てみます。

期中さまざまなな要因で、
日経平均は変動しますよね。

全体のトレンドは、
どんな感じだったのでしょうか？

Excelで移動平均を作る場合、
まず日経平均のデータを集めます。

日経平均のデータは、
こちらのサイトでコピペしたものです。

H列に7日平均線の欄を作り、
AVERAGE関数を作ってコピペします。

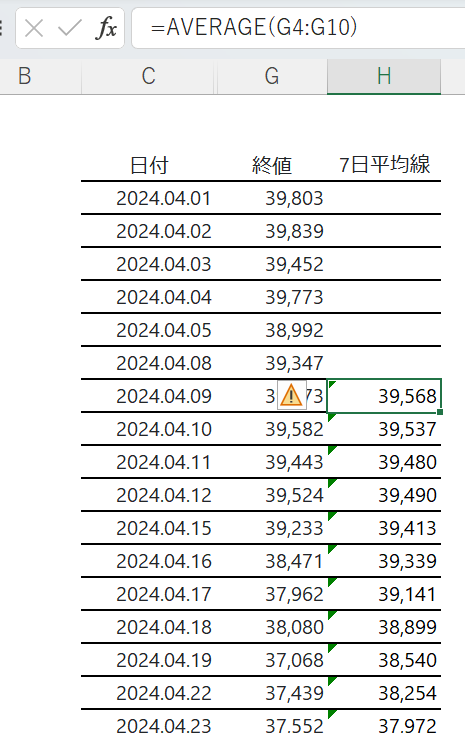
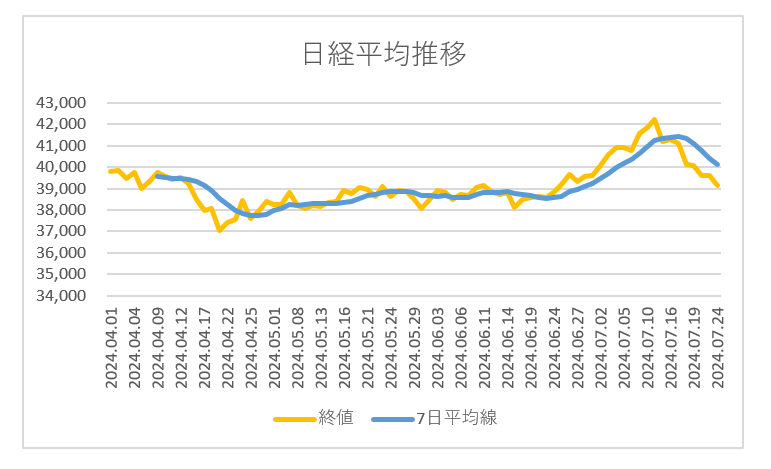
そこから折れ線グラフを作ると、
こうなります。

6月中旬から上昇トレンドですが、
最近は下降気味なのがわかります。

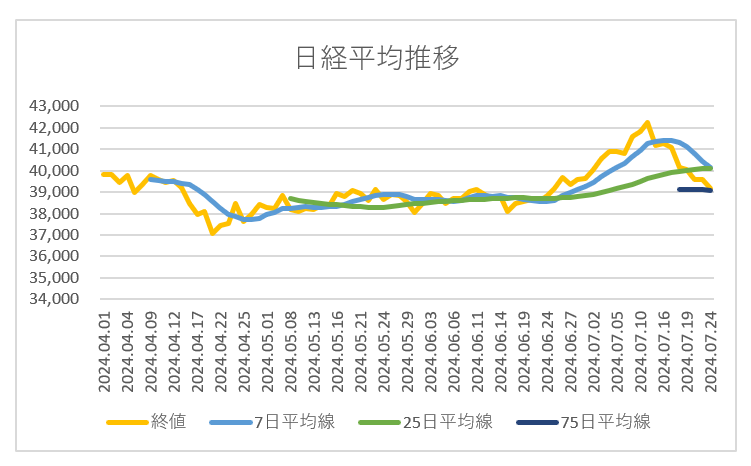
25日平均と75日平均を追加すると、
こうなります。

7日平均よりなだらかになり、
変動要因がさらに除外されています。

投資家は移動平均から相場を読み、
株の売買をしています。

いまは下落相場ですので、
つい売りたくなるところです。

しかし、
安く買って高く売るのが投資の鉄則。

つまり、
下落相場は逆に買うべきなのです。

怖い時こそ安心の買い場。
コチラの本に書かれています。

ご興味あればぜひご覧ください。

【株式投資2年生の教科書】感想・レビュー （2024/7/18更新） はじめまして、はるパパです。 さて本日は、コチラの本をご紹介します。 『株式投資2年生の...

第5章：日常に「統計学」を取り入れる

第5章で参考になると思った箇所、
コチラです。

本書では、
以下の二項分布例が書かれています。

まず、
成功回数と失敗回数を入力します。

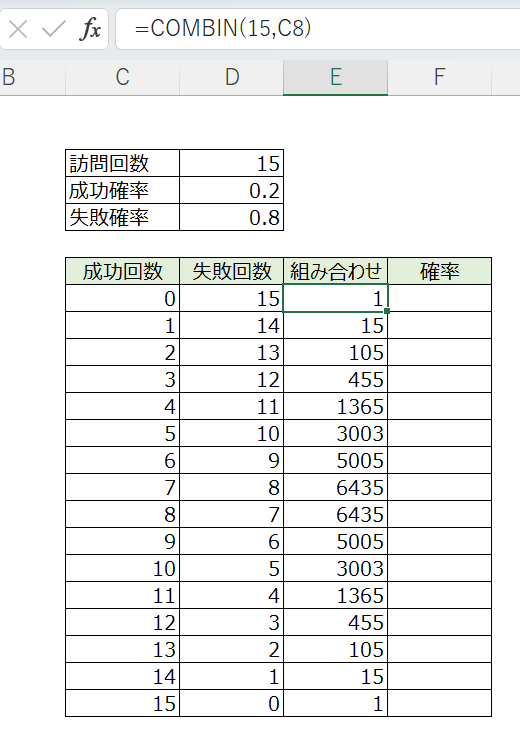
次に、
COMBIN関数で組み合わせを数えます。

たとえば成功回数＝1の場合、
訪問回数1～15のどこかで成功なので、
組み合わせは15通りですね。

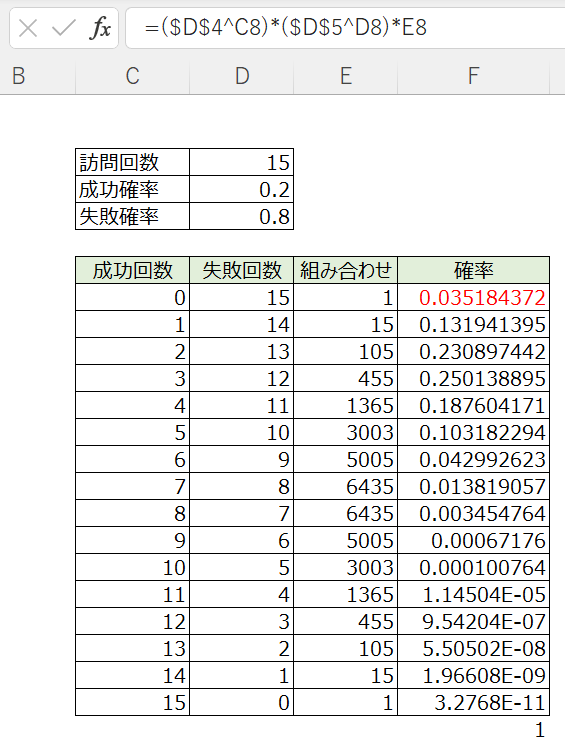
最後に、
確率を計算します。

Excel関数はただの掛け算です。

たとえば赤字の場合、
③＝確率となります。

①成功確率×成功回数
②失敗確率×失敗回数
③①×②×組み合わせ

5回以上成功する確率は、
5回～15回の確率を足せばよい。

5～15回の確率を足すと、
0.164…なので16.4%となります。

二項分布を覚えると、
さまざまな確率計算に使えます。

たとえば製品の品質検査で、
不良品が発生する確率がわかります。

他には新商品を市場に投入した場合、
成功確率の予測にも使えます。

仕事で確率計算ができれば、
予測精度が上がるので一目置かれます。

ぜひご活用ください。

まとめ

各章で参考になると思った箇所、
まとめました。

第1章：「割合」で目標を可視化する

第2章：「相関」が見えれば未来がわかる

第3章：「データ」を正しく読み解く

第4章：直近のトレンドを読む

【株式投資2年生の教科書】感想・レビュー （2024/7/18更新） はじめまして、はるパパです。 さて本日は、コチラの本をご紹介します。 『株式投資2年生の...

第5章：日常に「統計学」を取り入れる

まとめ

①～⑤を見ると、
何か難しく聞こえますよね。

①幾何平均
②散布図/回帰分析
③ヒストグラム
④移動平均
⑤二項分布

でも本書を読み進めると、
意外と難しくないことに気づきます。

自分で計算するのは難しくても、
Excelを使えば簡単に計算できます。

Excelで計算する場合のポイント、
それはExcel関数です。

昔は用途に応じて関数を覚えないと、
なかなか使いこなせませんでした。

Excel関数の本は調べるのが手間だし、
ピンポイントで知りたい関数がわからず。

でもいまは、
ChatGPTにEXcel関数を質問すれば、
ピンポイントで関数を教えてくれます。

なので、
どのようなケースで①～⑤を使うか？

これさえわかれば、
Excel関数をChatGPTで調べて、
Excelに入力すればよいのです。

これで予測の精度が上がり、
仕事の評価も上がるのですから、
ChatGPTとExcel関数を使う方がお得！

私もExcel関数は苦手ですが、
本書の通りやったら簡単にできました。

①～⑤で分析や試算しました、
と仕事で言えたらカッコいいですよね。

①～⑤を自由自在に操れる人、
仕事であまりいないですので。

間違いなく一目置かれますし、
評価が上がるのは間違いない。

Excel関数が苦手な方。
Excel関数を仕事に役立てたい方。

いますぐ本書をお買い求めください。

本書のお値段は990円、
本書はコチラ（↓）から購入できます。

・仕事に役立つ数学: AI時代に差がつく

お問い合わせ｜子供へのお金の教育 (children-money-education.com)

この記事を書いたのは・・・

はるパパ

• 小学4年生のパパ
• 子どもの教育（世界一厳しいパパ塾？）、ブロガー、投資家
• 投資の悪いイメージを払拭したい（難しい、怪しい、損する）